小更新，这次更新了连续买入时，买入量相对上次买点的乘数。

设成本价为a，当前价格为b，持有数量为X，需要买入的数量为Y，买入后的成本为c，则有：

$aX+bY=c(X+Y)$

设定的卖出增长率为i，设定的相对增长量的百分比为p，则有：

$c=(1+p*i)*b$

根据上两项，可知乘数m的公式如下：

$m=\frac{a-c}{c-b}=\frac{a-(1+p*i)*b}{(1+p*i)*b-b}$

举例来说，如果设定的卖出增长率为25%，百分比为10%，则在连续买入点买入持有量乘以乘数m的量后，买点的成本会控制在-2.5%以内。理论上来说，如果有无限的金钱，只要卡片未来的增长率到达2.5%，就可以收回之前所有的损失，这是一个简单的成本控制。

为什么要用这个乘数呢，这次的疫情大爆发，使得全球指数进入了下行通道，而且似乎看不见尽头，但短期来看，指数的震荡幅度达到了极致，美股3月4%上下起步的表现令人咋舌，所以，既然各国都在忙着救市、救经济，这段时间的指数注定是史诗级的强烈震荡，何不控制好成本，然后从中获利呢？于是就有了这个乘数。在资金有限的长期定投中，这个乘数能标示出100%投入时，实际需要投入的量，便于继续按情况追加投入，所以我也把它加到了bPoint的图表里。

当然这是一种高风险的实验，个人的资金不可能是无限的，所以需要一些限制来降低每次操作的风险，第一是找到好卡片，这个之前已经做好了，第二是选取当天跌幅超过5%的卡片，先投入一点点，然后等待，当再次大跌的时候，继续补充，直到下次反弹时一次性卖掉，这个逻辑下，我目前持有的资金能承受2-3次的大跌，这样的操作应该能持续到各国政府的救市措施最终出清完毕。然后也许是漫长的等待，等待疫情退去，经济复苏之后，再回到长期定投的逻辑。

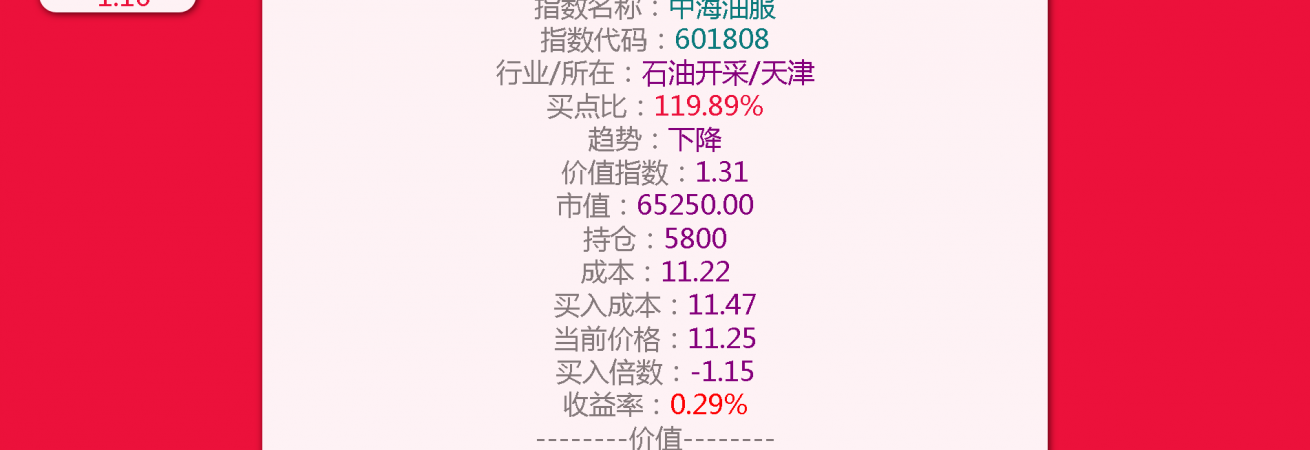
根据这个逻辑，买入了实验性的第一张卡片，中海油服，今天跌了5%多一点，明天会怎么样呢，希望是好的吧w

以上。